在微观尺度下,物体之间的表面力远大于重力等体积力,非常容易发生接触粘附:两个靠近的物体将会因表面力的存在而难以分离。对于干燥、不带电的表面,表面力一般由范德华力主导。由于范德华力对于运动的阻碍和限制作用,在设计机械部件,特别是微观尺度下的机械部件时(如微机电系统MEMS),研究人员往往通过增加相邻表面的间隔距离来减小或规避界面间的接触黏附,从而使部件得以流畅运动,不会被“卡住”。
但是否有可能反过来利用这种界面粘附效应来驱动微观机械系统呢?近日,西湖大学仇旻教授团队提出了一项光操控技术,成功利用范德华力实现微米片的光控振荡运动。其中,光信号作为激励源,通过光热效应对机械系统的杨氏模量和哈梅克系数进行调控,在范德华粘附力的作用下可实现微米片百千赫兹频率的振荡控制,且振幅控制精度达到纳米量级。相关研究工作以“Light-Controlled Oscillation of Microplates Leveraging Contact Adhesion”为题发表于ACS Nano。仇旻教授团队博士后、现国科大杭州高等研究院副研究员唐伟伟,以及浙江大学-西湖大学联培项目博士生贾倩楠为共同第一作者。西湖大学仇旻教授,研究员严巍为文章的通讯作者。

论文链接:
https://pubs.acs.org/doi/10.1021/acsnano.5c09198
1
光控振子的结构设计:
微光纤+微金片构成“微悬臂”
要实现机械结构的振荡运动,则需要定义机械系统的约束,并释放特定的自由度。悬臂梁是常见的实现振荡运动的基本部件。对于平面接触的情况(图1a),在微观尺度下,表面力的作用效果远大于重力。在平面衬底上伸出的悬臂由于不受到表面力的作用(伸出的悬臂不再靠近任何一个表面),将继续保持平直伸展状态,不发生明显形变(重力作用影响较小)。
当我们将平面衬底置换成曲面衬底,其上附着的悬臂结构将不再平直伸出,而是发生线性下垂(这里假设衬底在悬臂下方):也就是说,悬臂将会沿靠近曲面衬底的方向,发生线性空间分布的弯曲形变,如图1b所示。这是因为悬臂受到了弯曲衬底施加的范德华力的作用(图1c上图)。其中,衬底对悬臂施加的范德华力即为悬臂所受的载荷,它具有短程力的基本特征,在界面间距很近时表现为排斥力(PvdW>0),在界面间距较远时表现为吸引力(PvdW<0),且作用力强度随间距增加而迅速衰减。由于范德华力是短程作用力,且原本平直伸出的悬臂无法完全贴合曲面衬底的弯曲表面,从而使悬臂等效只在很窄的接触区域内(标记为lct的阴影区域)受到范德华力的作用,而在该接触区域外可视为自由不受力的状态(重力对形变的影响可忽略)。因此,在超出接触区域的范围外,悬臂的形变将表现为线性下垂。
研究人员利用结构力学模型,仿真了不同几何参数下曲面衬底上长度为20 μm,两翼对称分布的微悬臂末端的挠曲程度(Wend),如图1d所示。可以发现,当悬臂厚度较薄(百纳米量级),且弯曲衬底的曲率半径为1-2 μm时,微悬臂末端的挠曲程度可以达到几十到百纳米量级。
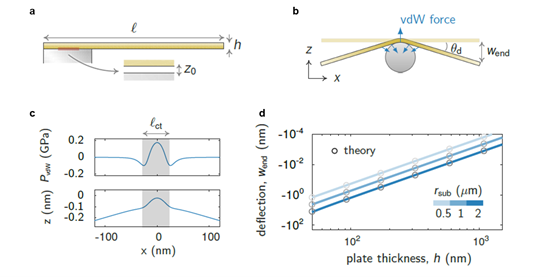
图1. 光控振子的基本结构和形变状态。a.平坦衬底上伸出的悬臂及其形变状态。b.弯曲衬底上伸出的悬臂及其形变状态。c.弯曲衬底上微米片/悬臂的载荷情况(上图)及挠曲(下图)。d.弯曲衬底上微米片/悬臂末端挠度与光控振子几何参数的关系。几何参数包括弯曲衬底的曲率半径,以及微米片/悬臂的厚度和宽度等。
研究人员将熔融拉锥得到的微光纤作为衬底,以微米金片作为悬臂搭载在微光纤上,即形成了一个简易的悬臂结构。该机械系统满足弯曲衬底+微米薄片的基本组成。另一方面,由于微光纤能够对光信号进行传输,并以倏逝场的形式和其上附着的金片发生相互作用,产生光热效应,该悬臂系统的形变状态因此可受到光源开关状态的调节(图2a)。
2
光热激励改变悬臂形变状态
对于图2a所示的微悬臂系统,其悬臂/微米片线性下垂的角度与微光纤、微米片的几何尺寸,以及材料和力学参数都息息相关。其中,重要的力学参数包括悬臂的杨氏模量以及光纤-金片接触界面的哈梅克系数(用来表征范德华力的强度)。根据欧拉-伯努利梁方程以及赫兹接触定理,研究人员推导得到了微米片下垂角度的表达式:
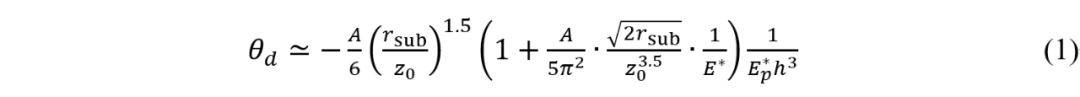
除了几何参数外,A和E分别对应接触界面的哈梅克系数,光纤-金片系统整体的等效杨氏模量(E*)以及金片的等效杨氏模量(Ep*)。这两个物理量都是温度的函数,也就是说,它们将受到光热效应的调制。当光源分别处在开启和关闭状态时,悬臂对应不同的温度。相应的,该光控振子中的杨氏模量,以及接触界面上的哈梅克系数也会发生改变,并因此导致悬臂下垂角度的变化,如图2b所示。
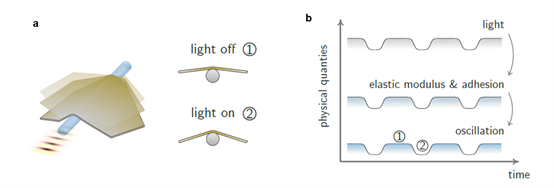
图2. 光控振子的运动机理。a. 基于微光纤-微金片系统的光控振子受光开关调制发生振荡运动。具体表现为悬臂/微金片在“开光”和“关光”时具有不同的形变状态。b. 微光纤-微金片系统中,金片的杨氏模量以及光纤-金片接触界面上的范德华力强度受到光热效应的调制,进而使得悬臂/微金片在光源开启和关闭时展现出不同的挠曲,进而实现光控振荡。
3
低频扑翼运动与高频共振模式
利用数字全息显微镜(见图3a),研究人员可以对光控振子悬臂的面外位移进行实验测量,并对其空间分布进行表征。根据实验观测现象的不同,研究人员将实验结果按驱动频率进行分类:在光信号频率较低时,悬臂整体形变的空间分布呈线性,表现为扑翼运动;当光信号频率较高时,悬臂的本征振荡模式被激发,并呈现出更加复杂的空间分布。
对于图3b展示的微光纤-微金片系统,其上三点的面外位移受低频光信号(1 Hz)的调制结果如图3c所示:当光源开启时,金片上各点统一向靠近光纤的方向发生运动,也就是说,下垂角θd的绝对值增加;当光源关闭时,金片上各点恢复原位。因此可以猜测,该光控振子系统中,哈梅克系数随温度的升高而升高,或杨氏模量随温度的升高而降低(见公式(1))。
另一方面,金片悬臂上各点净面外位移的空间分布整体呈线性,并关于光纤-金片接触线对称(图3d),这证明了范德华力作为短程力是使悬臂发生形变的主导外力。通过理论仿真,研究人员进一步排除了重力、光力以及热膨胀带来的影响。
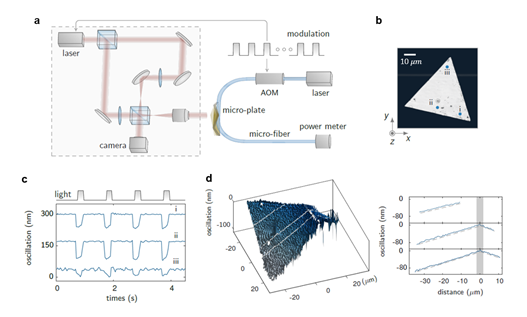
图3.低频扑翼运动。a. 数字全息显微镜(左)和驱动光路(右)示意图。b.微光纤-微米金片系统灰度光镜图。c. 金片上三个点(b图标记)的面外位移与输入光信号(重频1 Hz,占空比20%)的关系。d.开光时微米金片各处净面外位移的空间分布。
对于图4a所示的微光纤-微金片系统,当激励光源的重复频率较高时,可以激发出光控振子的本征振荡模式(图4b的三个框图)。同时,随着激励光源频率的变化,振子振动的空间分布也会相应发生演化,并在高阶模式下呈现出多个振动反相区,以及波节和波腹。研究人员利用频率扫描方法,通过捕捉振子振动信号突然出现的尖峰来定位振子的谐振频率(图4c)。以110 kHz下的本征振荡为例,该本征模式的品质因子约为20.1。其上五个点(见图a)振荡运动随时间的关系如图4d所示。可以看到,点1、4和点2的运动反相,这对应了图4b中相应频率下振荡运动的特殊空间分布。另一方面,研究人员发现,振荡运动的振动幅度随输入光功率的增大而呈线性增长趋势。这一现象在低频和高频下均稳定出现,且通过功率实现的振幅调控精度在纳米量级(图4e)。
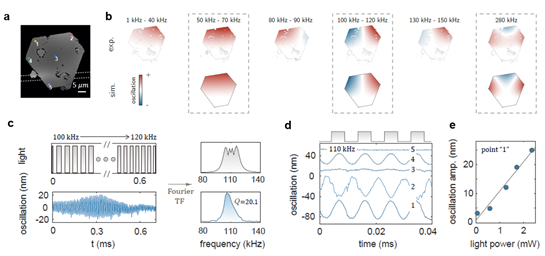
图4.高频共振运动。a.数字全息显微镜拍摄得到的微光纤-微米金片相位图。b. 实验测量(上图)和仿真计算(下图)得到的不同频率下的振动模式。c. 左:100 kHz-120 kHz的扫频信号(上图)和实测振动信号(下图)。右:扫频信号(上图)和振动信号(下图)的FFT频谱。d. 100 kHz共振频率下,金片上五个点(见b图)振荡运动随时间的关系。e.点“1”的振幅随输入光功率的变化。
4
总结与展望
综上所述,该研究将通常被视为运动“障碍”的接触粘附力转化为有效的驱动力,通过光热效应实现了对微米级结构的振荡运动操控。其中,光控振子结构简单,易于制备,且具有高频响应,纳米精度等优势,为微型机器人、光学微振镜等领域的应用提供了全新的思路。考虑到目前尚缺乏在微观尺度下对范德华力和材料模量进行原位测量的可靠实验方案,这项工作有望通过建立振子形变和哈梅克系数、材料杨氏模量的映射实现对相关物理量的定量表征。
文章来源:西湖大学工学院官方公众号
https://mp.weixin.qq.com/s/lfO-b4Ao_yhzocghTQzEsw

