撰稿人 | 张磊
论文题目 |Optical steelyard: high-resolution and wide-range refractive index sensing by synergizing Fabry–Perot interferometer with metafibers
作者 | 张磊,尚兴港,曹思敏,贾倩楠,王纪永*,严巍*,仇旻*
完成单位 |浙江大学电子信息工程学院,全省3D微纳加工和表征研究重点实验室,浙江西湖高等研究院,西湖大学光电研究院,杭州电子科技大学电子信息学院
研究背景
光纤传感器因质量轻且能进行实时监测而被广泛研究。根据光与物质发生相互作用的区域,光纤传感器可以分为侧壁集成和端面集成。为适应器件小型化发展的趋势,光纤端面集成式传感器(Fiber Tip Integrated Sensor,FTIS)表现出更强的竞争优势,尤其在复杂且狭小的环境中。因此,FTIS在许多领域得到应用,例如温/湿度检测、生物医疗传感以及气体或液体混合物浓度标定。在上述的应用中,外界的刺激将引起折射率的改变,故折射率分析是一类最基本的探测手段。
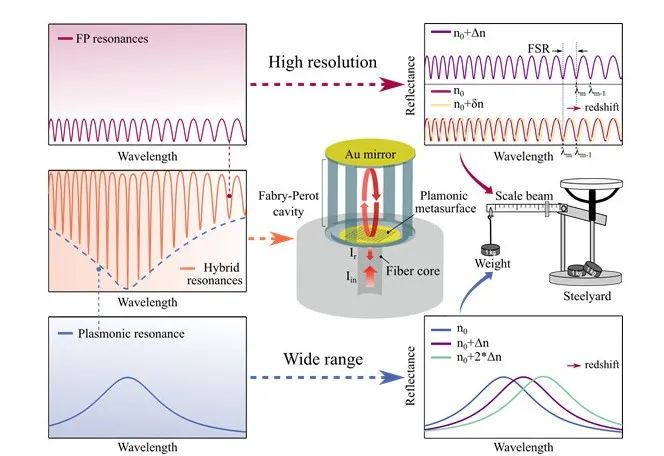
通常,灵敏度、分辨率和线性传感量程是评价传感器性能的三个重要指标。其中灵敏度可定义为单位折射率变化所致的谐振波长偏移量:S=Δλres/Δn。分辨率(Figure Of Merit,FOM)定义为归一化灵敏度,反映了测量的精度,通常用灵敏度除以光谱的半高全宽,即FOM =S/FWHM。又由于FWHM与光谱的品质因子(Quality factor,Q)相关,即FWHM=λres/Q,因此FOM=S×Q/λres。线性传感量程,通常与自由光谱范围(Free Spectral Range,FSR)相关,它反映了传感器的有效工作范围。在此范围内,即使折射率变化很大,也无需对折射率响应做二次校准,因此简化了数据采集及处理流程。理想情况下,人们希望FTIS同时具备高灵敏度、高分辨率以及宽的线性量程。但是对于大多数的折射率传感器而言,高分辨率与宽线性量程像“鱼和熊掌”一样,不可兼得。
杆秤是一种宏观尺度的测量物体质量的量具,人们经常用它来称量各种商品。杆秤历史悠久,最早可追溯至战国时期。随着历史变迁,杆秤的外形演变出多种形式,但都具备两个要素:一个是用来刻画测量范围的砝码,另外一个则是具有精细刻度的秤杆。在称量中,可先通过砝码粗略地读取待测物的质量范围,然后通过移动秤杆上的游标,使砝码与待测物处于平衡,进而读取待测物质量的精确数值。如果粗估范围偏小,游标遍历了所有刻度后,仍然无法使砝码与待测物处于平衡,则可以用过增加砝码,扩大粗估范围,然后再遍历游标,从而读取待测物的质量。杆秤的称量过程体现了高分辨和宽线性量程的完美结合。如果能够将这种“砝码+秤杆”组合思想应用在折射率传感,是否有可能实现兼顾高分辨率和宽线性量程的传感器呢?
论文导读
在光纤端面集成等离激元超构表面可激发等离激元谐振(Surface Plasmonic Resonances,SPR)。由于宽线性量程和免标记的特点,SPR式的FTIS得到了广泛的研究和应用。然而,SPR的灵敏度通常较低,仅为几百nm/RIU,并且由于固有的欧姆损耗,其Q值相对较低。相反,光纤端面集成的介质类的法布里-珀罗干涉仪(Fabry-Perot Interferometer,FPI)可支持高Q的谐振,进而提供较高的分辨率。但是FPI类型的传感器工作范围受限于有限的FSR,量程较窄。这种局限源自Q值和FSR之间的权衡。它们互成反比,并且由精细度(Finesse,F)相互关联,即F=FSR×Q/λres。因此,一旦F确定,FSR通常与腔长成反比,而Q与腔长成正比。
此前的研究表明,通过级联两个光学路程长度稍有差异的干涉仪,可引入光学游标效应(Vernier Effect),从而在不损失Q的前提下增大FSR。然而,光学游标效应只是提高了灵敏度及分辨率,而工作范围却没有得到本质提升。开发兼具高分辨率和宽线性范围的FTIS仍然十分具有挑战性。
主要研究内容
鉴于此,本研究提出并演示了一种高性能的 FTIS。通过基于光纤端面的聚焦离子束刻蚀工艺(Focused Ions Beam milling,FIB)及双光子光刻工艺(Two Photon Photolithography,TPL),在商用单模光纤跳线端面上集成了二维超构表面和三维FPI的复合结构。该复合结构是一个中空的三明治结构:底层是等离激元超构表面,与光纤结合形成超构光纤(metafiber);中间层是具有开放腔的聚合物基FPI;顶层是金的薄膜,如图1(a)第一行所示。为方便讨论说明,我们将这种复合结构命名为超构光纤FPI(metafiber-FPI)。光束作用在metafiber-FPI内可同时激发SPR和FP谐振。
由于传感过程与宏观世界中杆秤的测量原理十分相似,本文提出了光学杆秤机制。SPR谐振类比砝码,反映待测溶液的折射率范围,而FP谐振类比具有精细刻度的秤杆,提供待测溶液折射率的精确数值。通过协同具有宽FSR(低Q)的SPR谐振和具有高Q(窄FSR)的FP谐振,在实验中实现了分辨率达2664 /RIU,线性量程突破一个FSR的传感性能。本研究于2024年8月15日以“Optical steelyard: high-resolution and wide-range refractive index sensing by synergizing Fabry–Perot interferometer with metafibers”为题发表于 PhotoniX。
技术突破
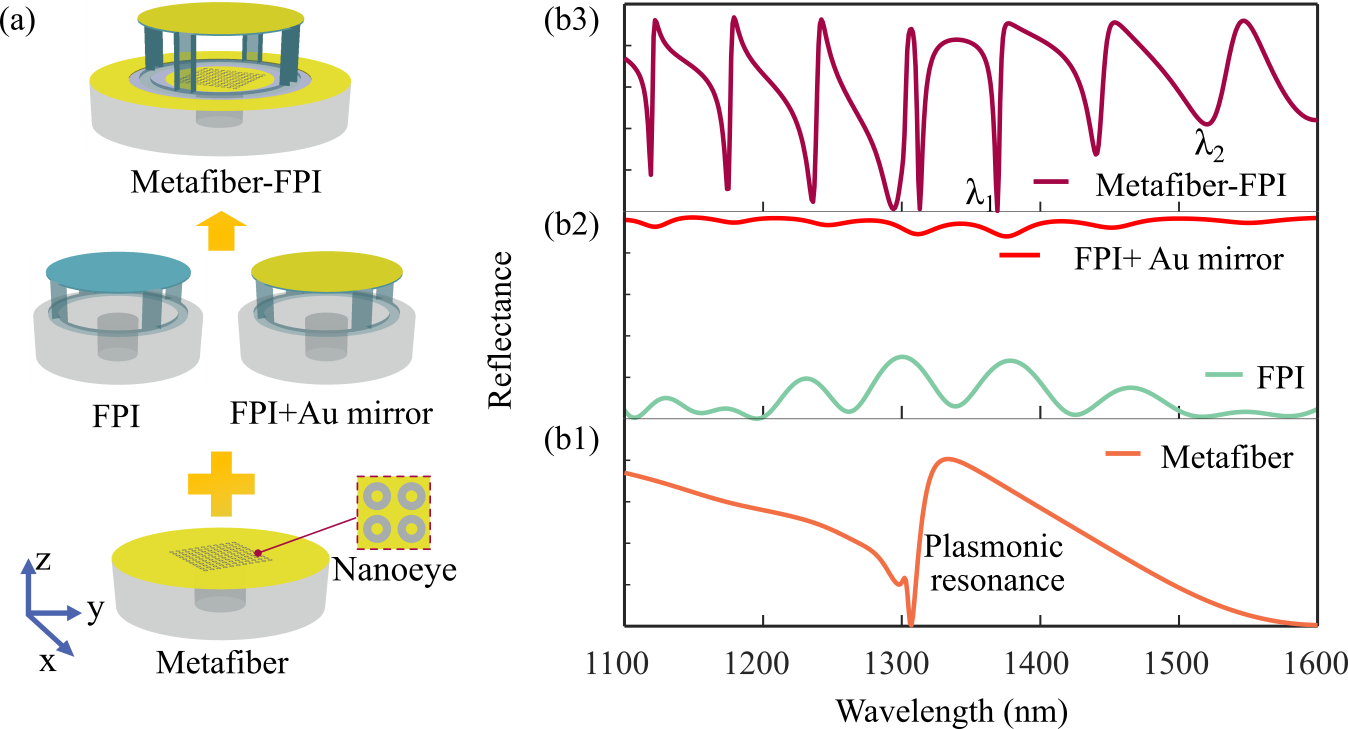
图1 Metafiber-FPI形成示意图(a)及对应结构的光谱计算(b)。
1探究metafiber-FPI高Q值的成因
如图1所示,相较传统介质类的FPI(b2中的绿色曲线),metafiber-FPI的Q值提升来自2个方面的原因。其一是底层等离激元超构表面和顶层金膜的引入,使得端面的反射率提高。因此,在同等腔长的情况下,精细度提升并显著提升了Q值。其二是SPR谐振和FP谐振耦合产生了具有法诺(Fano)线形的混合谐振。在混合谐振的形成过程中,SPR的辐射损耗被抑制,进一步提升了Q值。
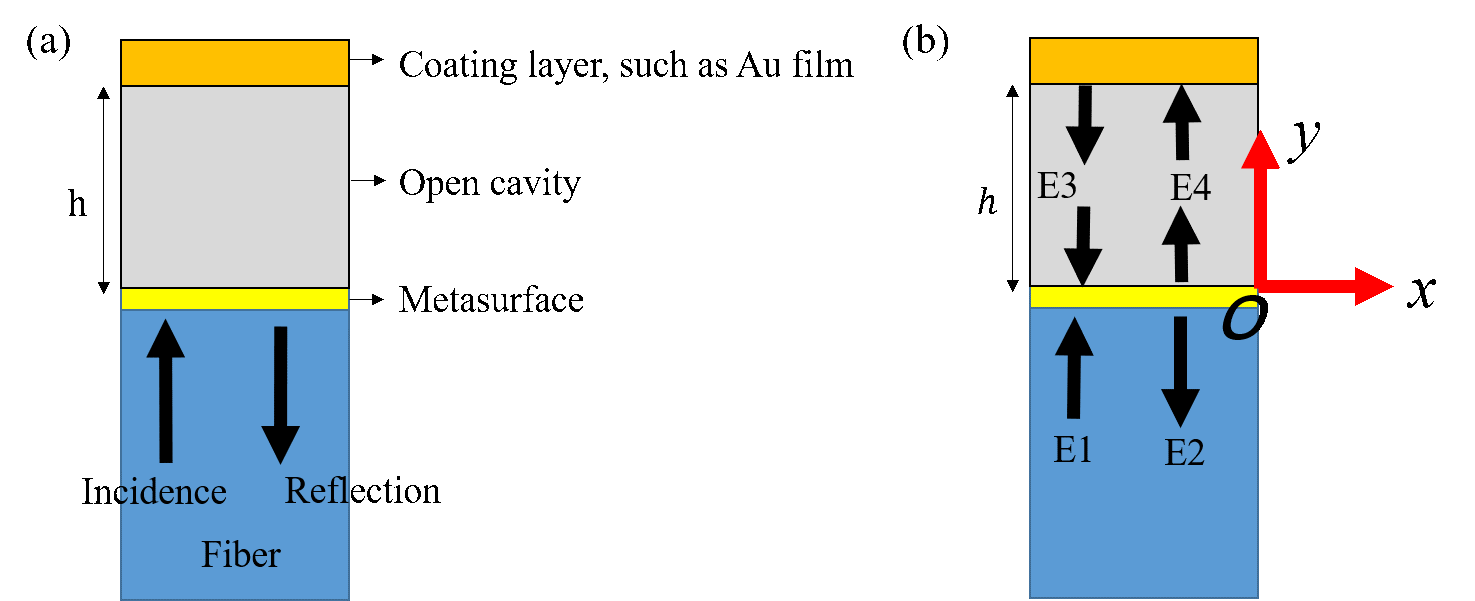
图2 (a)半解析模型的几何结构示意图。(b)在定义的坐标系中的多次反射示意图。
为了深入探究高Q值光谱的来源,同时快速求解不同腔长下及介质环境中metafiber-FPI的反射光谱,本研究还利用半解析模型对metafiber-FPI进行仿真。该模型将光与物质相互作用的物理过程描述为光在部分透明的纳米眼和顶部金反射镜之间的多次反射,如图2所示。借助COMSOL Multiphysics进行的纯数值计算,往往需要数小时,而该模型简化了这一环节的计算(一行代码便可以求解),为优化metafiber-FPI的光学性能提供了一种省时的求解方案。
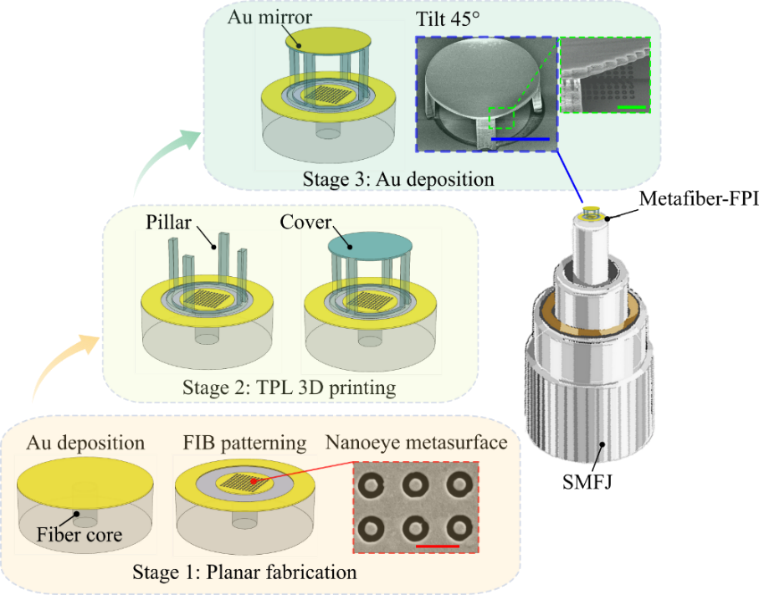
图3 Metaffiber-FPI的制备流程示意图,其中红色,蓝色和绿色比例尺分别为900 nm, 38 μm和3.5 μm。
2在光纤端面进行多维度集成
为了在单模光纤跳线的端面集成二维超构表面和三维谐振腔,形成用于杆秤传感的metafiber-FPI,本文基于课题组在光纤端面开发的非标微纳制备工艺,发展了如图3所示的工艺流程。
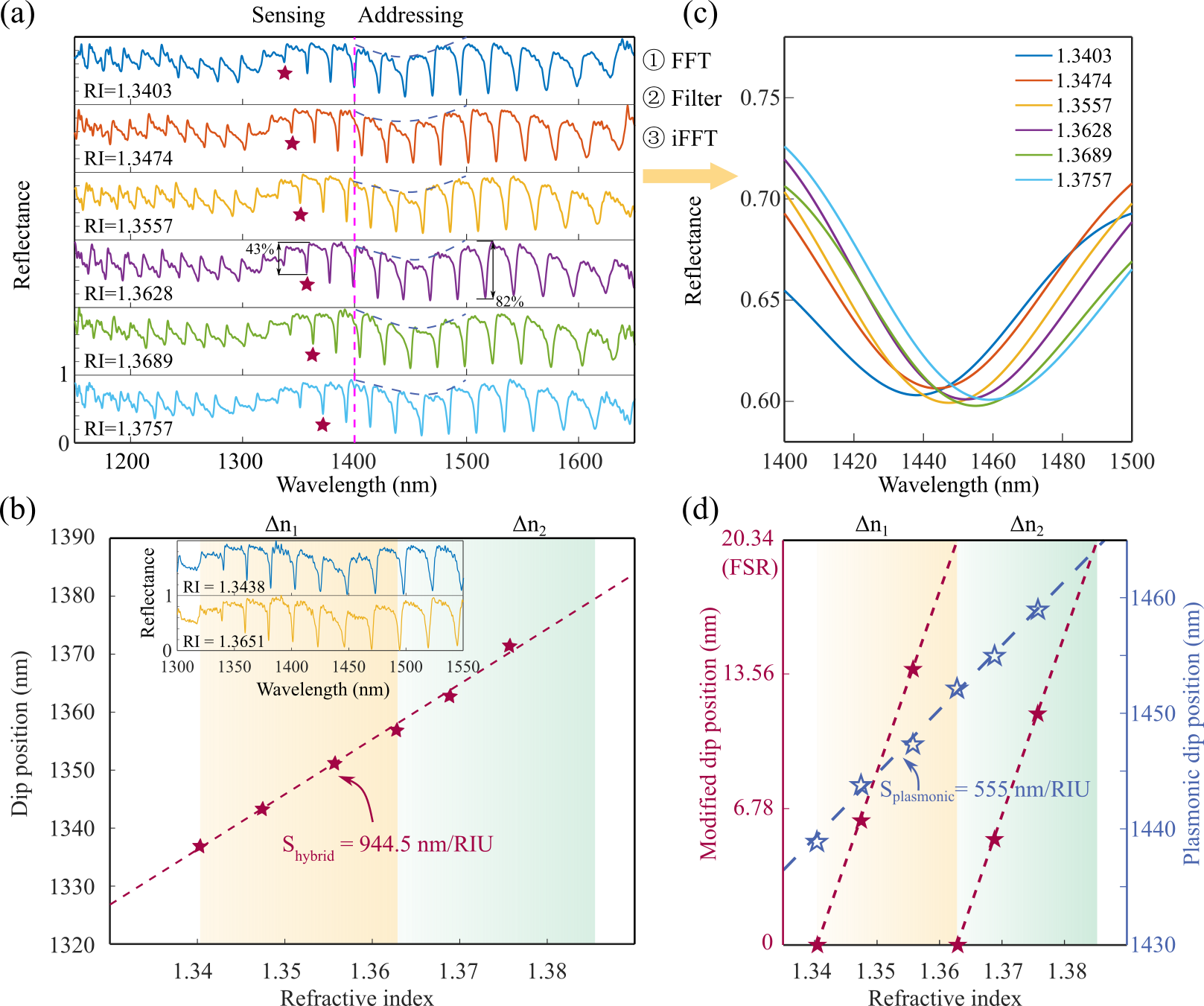
图4 傅里叶分析及杆秤传感图的建立。(a)Metafiber-FPI置于水-异丙醇混合溶液中的反射光谱。(b)Metafiber-FPI灵敏度提取。(c,d)对原始数据依次进行FFT、低通滤波以及iFFT操作,最终建立杆秤传感图。
3光学杆秤传感机制的建立
图4展示了混合谐振的谐振谷随溶液折射率的变化趋势。通过对数据进行线性拟合,可知红色星号标记的谐振具994.9 nm/RIU的灵敏度。然而,如图4(b)插图中的蓝色和黄色光谱所示,当光谱偏移量等于FSR时,混合谐振的谐振谷在传感区域几乎处于相同的波长位置,从而因无法分辨光谱而导致传感失效。这意味着高分辨率传感机制只能有效识别有限范围内的折射率变化,即存在有效折射率周期Δn。为了打破FSR对传感范围的限制,本研究通过傅里叶分析,对混合谐振中的SPR分量进行提取(图4(c))。由于SPR的谐振谷随介质环境的改变呈现单调而非周期性的变化,从而实现对折射率范围的判别(图4(d))。
观点评述
传统的FTIS很难同时实现高分辨率和宽线性量程。本研究通过将超构光纤和带有上层金反射镜的FPI结合起来,形成了metafiber-FPI结构,达到同时提升Q值并拓宽FSR的效果。利用FP谐振和SPR之间的模式耦合,成功地激发了具有Fano线形的混合谐振,从而在液体中实现了约为3829高Q值和约为2664 /RIU的分辨率。此外,本研究构建了半解析模型,成功分析了混合谐振的物理起源,深入理解了耦合系统的光学特性,并为验证数值结果提供了快速的求解方法。
通过傅里叶分析,本研究成功地从混合谐振中提取SPR分量,从而获得了宽的线性传感范围。在模拟和实验中分别实现折射率范围为1.330-1.430和1.3403-1.3757的精确测量,相当于传统FPI中四个和两个FSR光谱偏移的准确识别。
最后,成功演示了多维集成技术在单模光纤跳线端面的兼容性,展示了多维超构光纤的集成方法。同时,所提出的杆秤原理也为其他需要同时具备高分辨率和宽线性范围的光学元件,如芯片上的光谱仪,提供了研究思路。
本文出处
发表于:PhotoniX
论文链接:
https://photonix.springeropen.com/articles/10.1186/s43074-024-00138-3
文献检索:
PhotoniX 5, 24 (2024). https://doi.org/10.1186/s43074-024-00138-3

