Topology has brought novel physics perspectives and manipulation methods to optical research, with its hallmark achievement being the ability to enable unidirectional (reflectionless) and robust (highly tolerant to perturbations) transmission of light. Within this research domain, pseudo-spin-derived topological photonic crystals can achieve unidirectional, robust transmission of optical modes bound to pseudo-spin without breaking time-reversal symmetry. This compatibility with integrated optics applications and existing fabrication processes has spurred a series of important demonstrations, such as topological lasers and optical frequency combs, establishing it as one of the mainstream research paths for developing topological optics applications.

Currently, the design of pseudo-spin-derived topological photonic crystals is often realized by emulating specific condensed matter physics phenomena, which introduces several limitations. First is complexity: in many cases, researchers must meticulously construct an optical structure that mimics the behavior of a condensed matter system, much like building with blocks. Second is a lack of systematic approach: designing one optical topological phase requires referencing one specific condensed matter model; there is no general design methodology. More importantly, this approach cannot yield new insights that transcend the existing knowledge framework of condensed matter physics.

Recently, PhD student Tianyuan Liu, along with Professor Min Qiu and Researcher Wei Yan, from School of engineering, Westlake University, jointly proposed a design method for pseudo-spin-derived topological photonic crystals. This method, based on the inherent azimuthal dependence of coupling coefficients in the coupling relationships of angular momentum modes, successfully realized various spin-derived topological phenomena, including spin-valley Hall phases, anomalous spin-valley Hall phases, anomalous Hall phases in the spin subspace, and anti-helical edge states. This method not only exhibits a degree of systematicity and universality, with various corresponding optical designs being more concise and robust compared to existing reports, but also, guided by this method, the researchers reported new knowledge beyond the existing framework of condensed matter physics. This includes the discovery of a new anomalous spin-valley Hall phase, the proposal of a construction model for spin-valley Hall phases beyond the antiferromagnetic effect framework, and a construction model for anomalous Hall phases beyond the Haldane model.

The related research results were published in Nature Communications in the form of pure theoretical research under the title "Winding coupling phase for pseudo-spin-derived topological photonics."

Research Highlights:

Coupling Winding Number – The Topological Wrench

The researchers first observed an azimuthal dependence in the coupling coefficients within a system composed of two rotational modes, A and B, coupled via evanescent fields. To establish a topological description of this dependence, they assumed A is fixed while B orbits around A without rotating itself. As B completes one orbit and returns to its starting point, the coupling coefficient winds an integer number of times around the origin in the complex plane. This winding count is defined as the coupling winding number, W. Its essence is a homotopy topological invariant π1(S1) mapping from the orbital trajectory to the evolution trajectory of the coupling coefficient. Interestingly, borrowing the convention in photonic crystals of assigning rotational direction as pseudo-spin, the researchers found that the coupling winding number is inherently linked to this pseudo-spin: flipping the pseudo-spin (mode rotation direction) reverses the sign of W.

Introducing this topological invariant into an n-fold rotationally symmetric crystal composed of resonators A and B supporting angular momentum modes, they found that specific values of W can act like a wrench, "twisting" the phase of the eigen-wavefunctions at high-symmetry points in momentum space. This implies non-zero Berry curvature and locally non-trivial topological phenomena (sometimes seen in valley topology). Simultaneously, because W is inherently linked to pseudo-spin, this wrench produces Berry curvatures of opposite signs for opposite pseudo-spins at the same high-symmetry point, meaning the crystal's non-trivial topological phase will also be spin-locked.

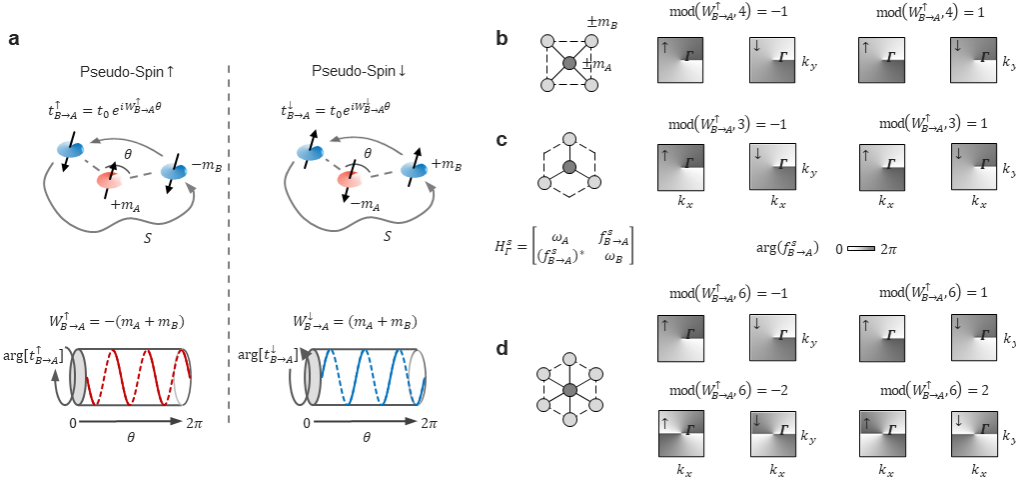
Figure 1: Coupling winding number: Definition, pseudo-spin-derived properties, and vortices in momentum space.

Spin-Valley Hall Phase

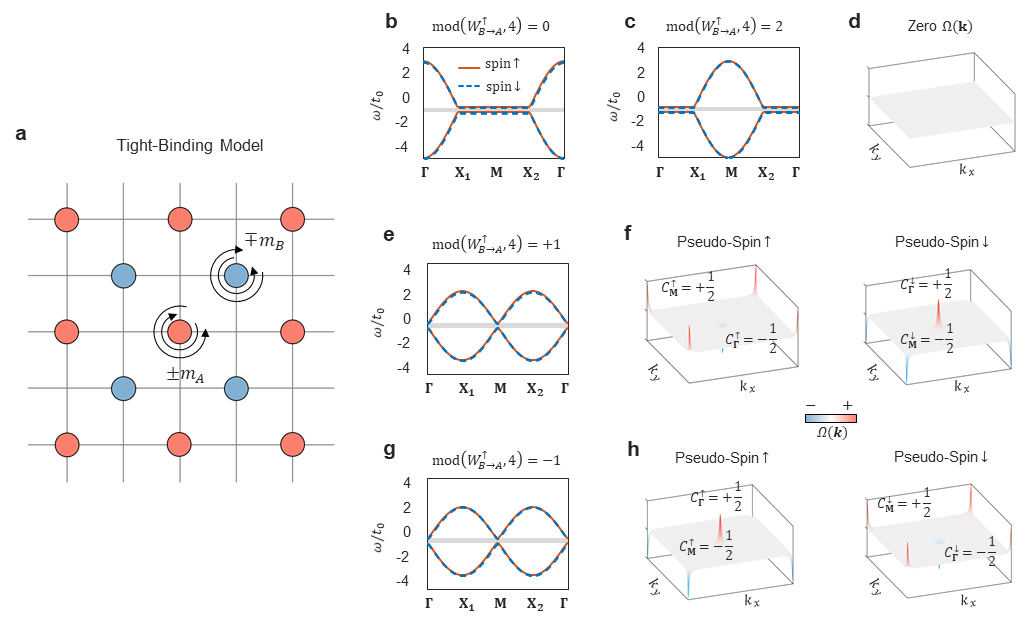
Figure 2: Spin-valley Hall phase realized in a 4-fold rotationally symmetric lattice.

For a 4-fold rotationally symmetric crystal composed of two sublattices, A and B, the researchers found that when mod(W,4)=±1 , the crystal exhibits a spin-valley Hall phase. Specifically, whether flipping pseudo-spin or flipping valley, the topological invariant defined by the spin-valley Chern number reverses sign. The spin-valley Hall phase was first proposed in antiferromagnetic materials within condensed matter systems. Realizing it in optical systems was considered challenging because simulating antiferromagnetic effects in optics is very difficult. By employing the coupling winding number as a topological wrench, one can move beyond the antiferromagnetic framework and achieve the spin-valley Hall phase in a concise and intuitive manner.

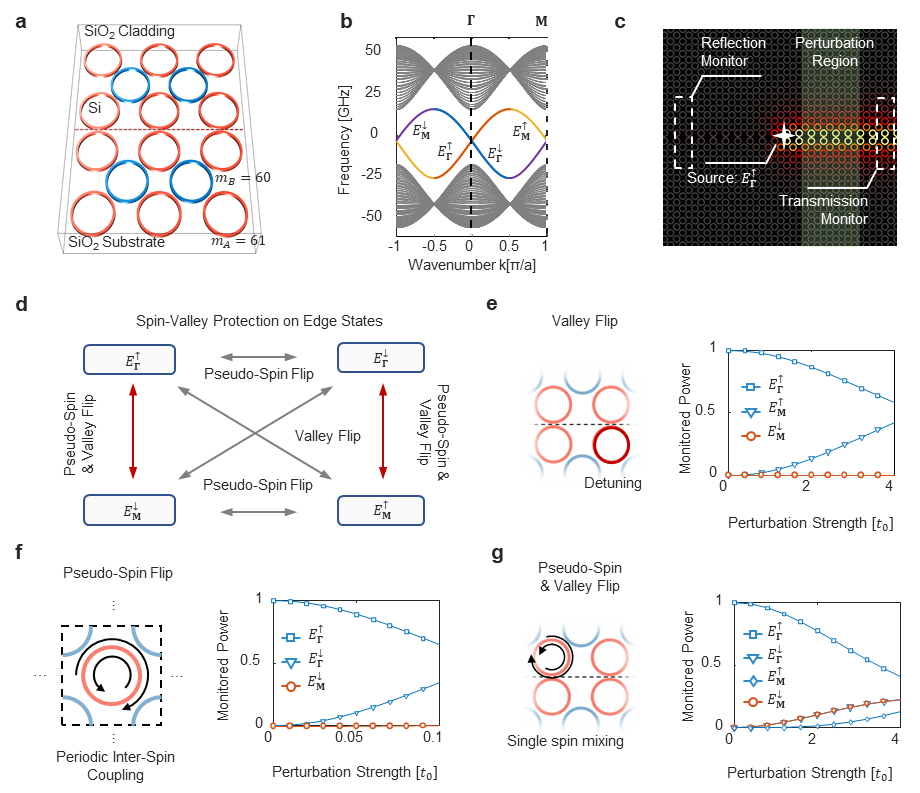
Figure 3: Optical spin-valley Hall phase realized on a Silicon-on-Insulator (SOI) platform.

The researchers provided a design on an SOI platform, using a microring array to realize the aforementioned spin-valley Hall phase. Unlike topological structures utilizing only spin or valley degrees of freedom, the spin-valley Hall phase provides dual protection for edge states: for two edge states propagating in the same direction, their pseudo-spin and valley degrees of freedom are opposite. Flipping only pseudo-spin or only valley cannot couple them; only simultaneously flipping both spin and valley can disrupt their orthogonality.

Anomalous Spin-Valley Hall Phase

Introducing the coupling winding number W into a 3-fold rotationally symmetric crystal composed of sublattices A and B, the researchers discovered a new anomalous spin-valley Hall phase. The anomaly lies in the fact that not only the Berry curvature of the valleys, but also the positions of the valleys themselves change upon flipping the pseudo-spin.

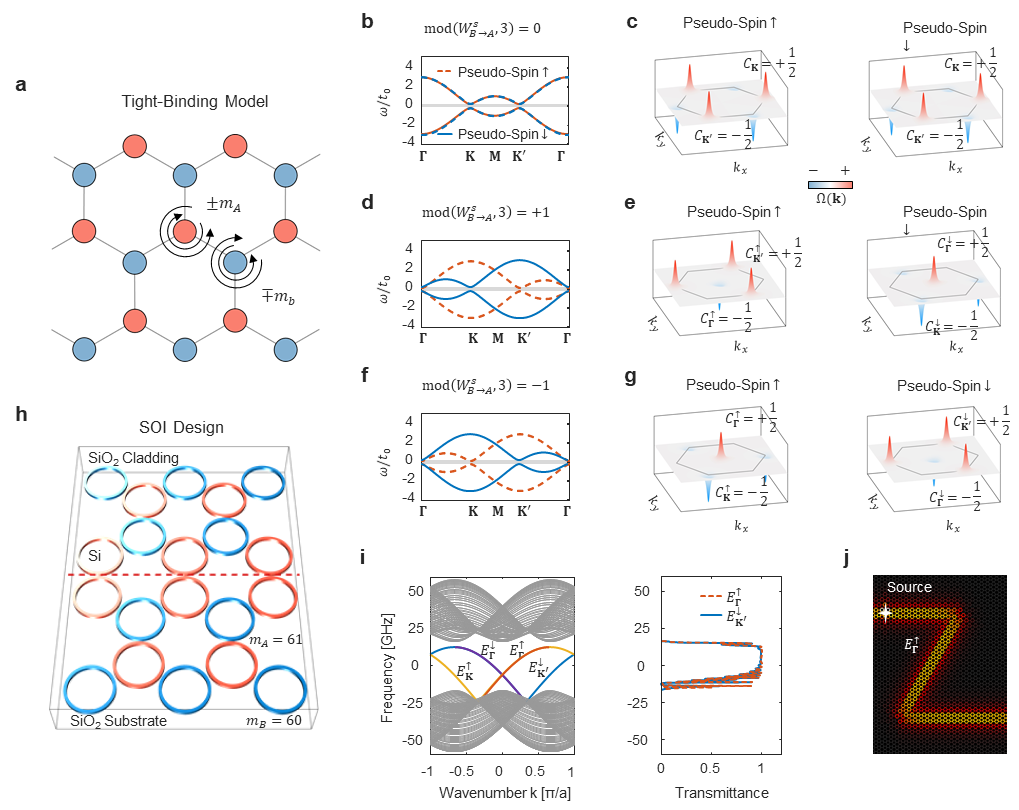
Figure 4: Anomalous spin-valley Hall phase realized in a 3-fold rotationally symmetric lattice and its optical design on an SOI platform.

Anomalous Hall Phase in Spin Subspace

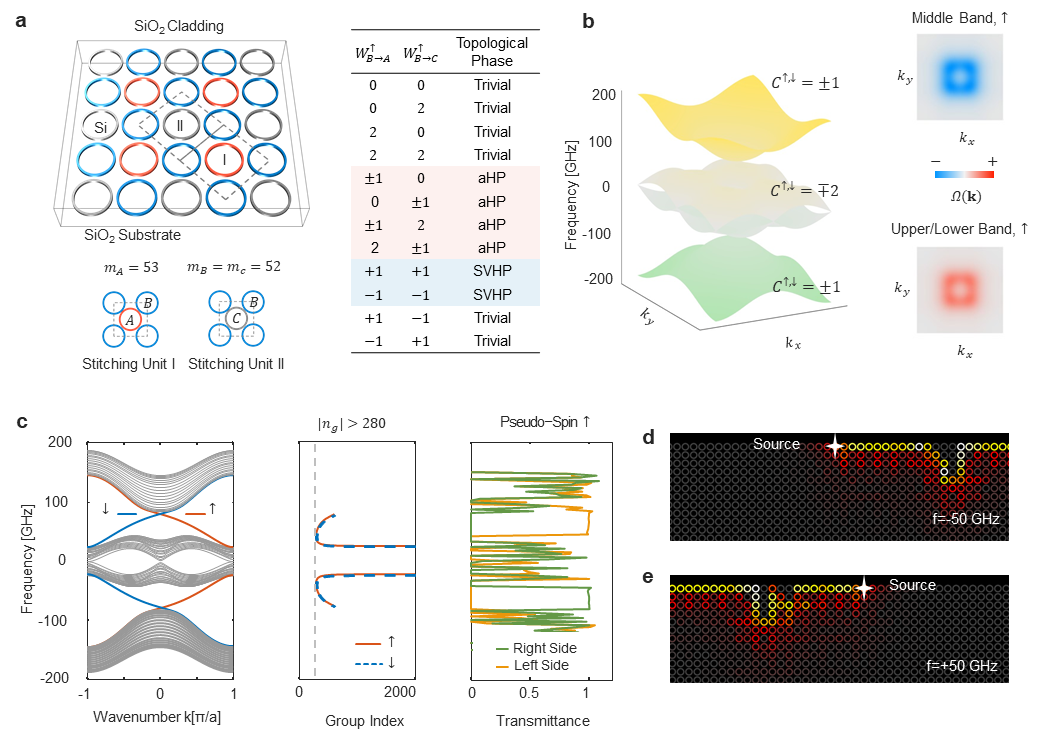
Figure 5: Optical anomalous Hall phase in the pseudo-spin subspace realized by combining coupling winding numbers.

The researchers also proposed a scheme to realize an anomalous Hall phase in the pseudo-spin subspace by stitching lattices. In this scheme, two coupling winding numbers jointly contribute to an equivalent magnetic flux that is non-zero within the sublattices but cancels out globally. This results in bands within the spin subspace having non-zero Chern numbers. The spin-locked topological edge states emerging at the boundaries of this crystal are not only robust against any defects that do not close the bandgap or break pseudo-spin orthogonality but also exhibit slow-light behavior with high linearity dispersion.

Anti-Helical Edge States

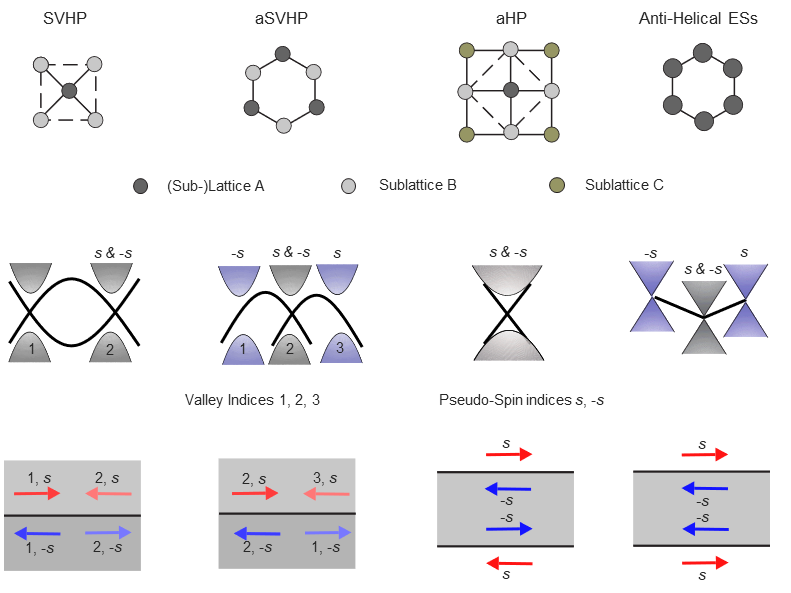
Figure 6: Summary of spin-derived topological phases realized based on the coupling winding number.

Using the coupling winding number, the researchers also realized a peculiar optical anti-helical edge state, previously seen in topological metals. Its characteristic is that edge states with the same spin propagate in the same direction on opposite boundaries of the same photonic crystal.

Key Achievements:

Discovered a homotopy topological invariant—the coupling winding number—inherently existing in the coupling relationships of rotational modes. Proposed that this concept can serve as a "topological wrench" for designing spin-derived topological phases, and based on this insight, constructed a systematic design method. This method moves beyond the common paradigm of designing spin-derived topological photonic crystals by emulating specific condensed matter phenomena.

Demonstrated a series of design schemes for spin-derived topological photonic crystals based on this method. These schemes collectively illustrate the systematic nature and a degree of universality of the method. Compared to corresponding existing designs, they are more concise (not requiring auxiliary microrings or introducing complex physical effects like nonlinearity) and robust (tolerant to misalignment of microring centers), holding promise for application in the development of related integrated optical functional devices.

Discovered a new anomalous spin-valley Hall phase; proposed a physical structure for the spin-valley Hall phase beyond the antiferromagnetic effect framework; and in the design of the anomalous Hall phase in the spin subspace, demonstrated a physical structure beyond the Haldane model. These demonstrations show that this method can yield new knowledge beyond the existing framework of condensed matter physics.

Tianyuan Liu, a PhD student in the Westlake University-Zhejiang University joint program, is the first author of this paper. Professor Min Qiu and Researcher Wei Yan of Westlake University are the corresponding authors. The research received support and assistance from Thomas Christensen (Technical University of Denmark) and Wenbu Duan (from the Jian Li group at Westlake University).

News Source:Official WeChat account of the School of Engineering (SOE), Westlake University

Paper Link:https://www.nature.com/articles/s41467-025-67627-2