A research team led by Professor Min Qiu at the School of Engineering of Westlake University has recently proposed a novel design method for controlling the dispersion properties of metasurfaces. Utilizing a feedback iteration strategy based on electromagnetic simulation results, this method successfully achieves high-quality metasurface dispersion designs. Compared to traditional dispersion design approaches, this work significantly enhances the performance of metasurface dispersion control. Furthermore, compared with numerous emerging inverse design methods, the proposed design model is notably more concise and easier to reproduce.

In terms of design outcomes, the paper demonstrates an achromatic metalens operating across an ultra-broadband range of 850-1800 nm, and a spectral router capable of focusing and splitting spectra linearly with wavelength within the 850-1550 nm band. The proposed method can be applied to various applications requiring control of optical field dispersion, such as achromatic imaging devices and spectral-resolving sensors. The related research findings have been published in *Laser & Photonics Reviews* under the title "Dispersion Design Method of Metasurface Based on Semi-Inverse Phase Matching".

**Link to the paper:**

[https://onlinelibrary.wiley.com/doi/10.1002/lpor.202500222](https://onlinelibrary.wiley.com/doi/10.1002/lpor.202500222)

Background & Method Details:

Metasurfaces exhibit intrinsic negative dispersion. Many practical applications necessitate deliberate design of their dispersion characteristics. Metasurface dispersion design methods can be categorized into three types: 1. Dispersion design integrating refractive elements, 2. Forward design, and 3. Inverse design. Among these, methods integrating refractive elements offer low design flexibility and result in large device sizes; forward design methods often yield devices with limited performance; while many inverse design approaches are often accompanied with issues such as device structures hard to analysis fabrication feasibility, complex models that are hard to reproduce, and high computational resource demands.

In this work, the researchers propose a semi-inverse design method based on phase matching. This method allows for an accurate analytical description of the target optical function. Moreover, by incorporating an iterative optimization process, it can correct design errors arising from the violation of periodic boundary conditions.

The proposed design method can be understood through the simplified flowchart shown in Figure 1. The input parameters for the design process consist of two parts. The first part involves building a meta-atom library. This requires designing meta-atoms of various shapes and sizes and calculating their phase dispersion responses via Finite-Difference Time-Domain (FDTD) simulations. The second part involves defining the target optical function (e.g., phase profile) according to the target device function.

After determining the input parameters, a gradient descent algorithm is used to arrange the meta-atoms according to the requirements of the target function, yielding an initial design layout. Subsequently, by evaluating the deviation between the simulated far-field energy distribution and the design target, theoptimization parameters are adjusted accordingly, making the design result gradually converge towards the expected outcome. High-quality final design results are obtained after several iterations.

A key innovation in this work's iterative optimization process is the introduction of the "nominal parameter" concept. Here, the parameters of the target function itself are treated as optimization variables. Appropriately adjusting the nominal parameters during each iteration ultimately resulted in design outcomes significantly superior to those obtained by traditional methods.

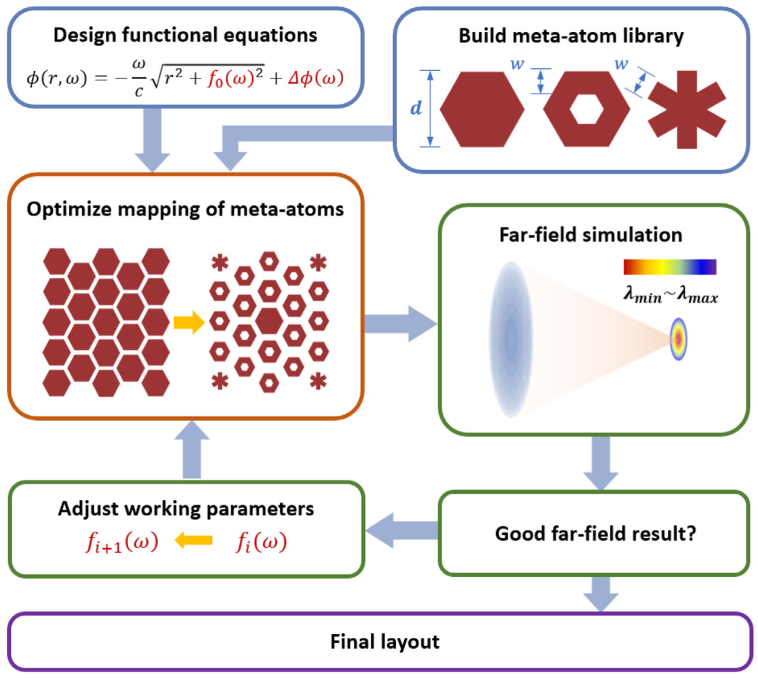
Figure 1. Simplified flowchart of the dispersion design method proposed in the paper.

Design Examples:

The paper presents two design examples. The first is an achromatic metalens operating in the 850-1800 nm band, with a diameter of 50 µm and a numerical aperture (NA) of 0.154 (see Figures 2 and 3). The second example is a spectral router operating in the 850-1550 nm band, with a diameter of 25 µm and a focal length of 75 µm (see Figures 4 and 5).

Achromatic Metalens: Figure 2b shows the layout of the designed achromatic metalens. The adjacent nanofins are arranged in a hexagonal lattice with a period of 680 nm and a height of 1 µm, made of silicon (Si). Figure 2c shows the focal length curve across the broadband range, demonstrating good agreement between the design result and the design target. Figure 2d shows the focusing efficiency and focal spot size curves across the bandwidth. The spot sizes indicate performance close to diffraction limit. Figure 3 shows the simulated far-field energy distribution for this achromatic metalens.

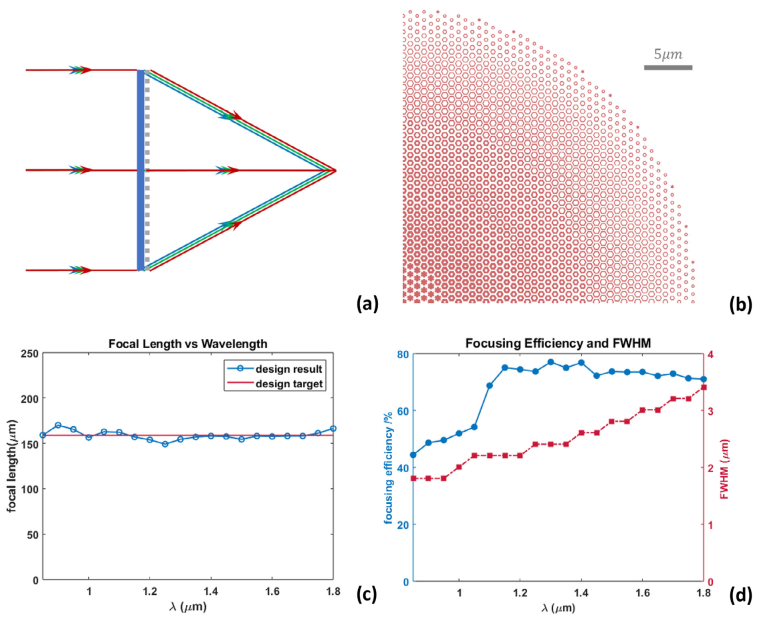
Figure 2. Functional schematic and performance data of the achromatic metalens.

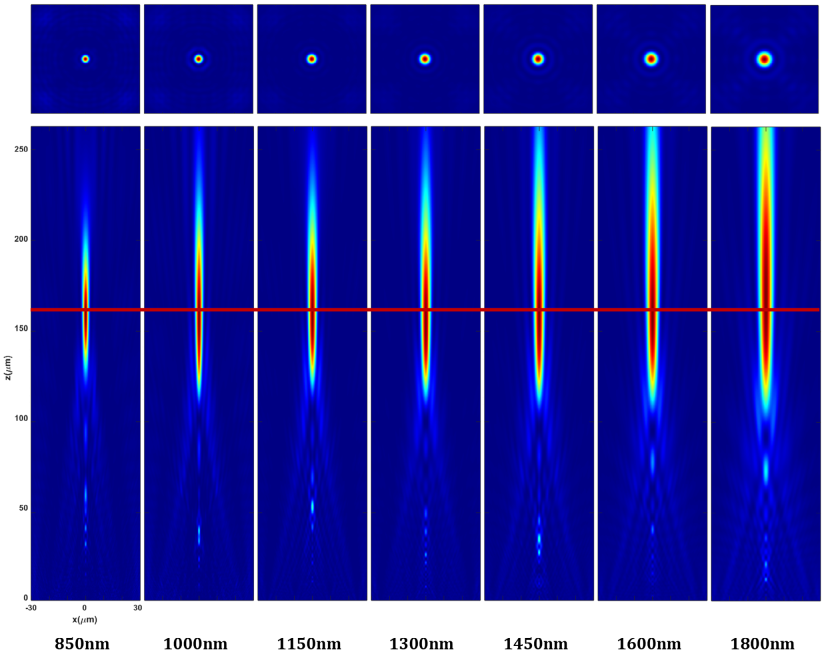
Figure 3. Simulated far-field focusing energy distribution of the achromatic metalens.

Spectral Router: The function illustration is shown in Figure 4a. Figure 4b shows the optimized arrangement of the metasurface units. The nanofin period, height, and material parameters are the same as in the achromatic metalens example. Figure 4c shows the focal positions and focusing efficiencies for different wavelengths. The controlled far-field diffraction energy distribution for this spectral router is shown in Figure 5. From Figures 4c and 5, it is evident that the focal points for different wavelengths are linearly distributed versus wavelength along the longitudinal direction on the focal plane according. Figure 4d shows a focusing efficiency of approximately 75% across the design band, along with the Full Width at Half Maximum (FWHM) spot sizes. As the device lacks rotational symmetry, the FWHM data are calculated for both the x and y directions. The FWHM sizes in both directions show positive correlations with wavelength, consistent with theoretical analysis. The focusing spot sizes in this design example also close to the diffraction limit.

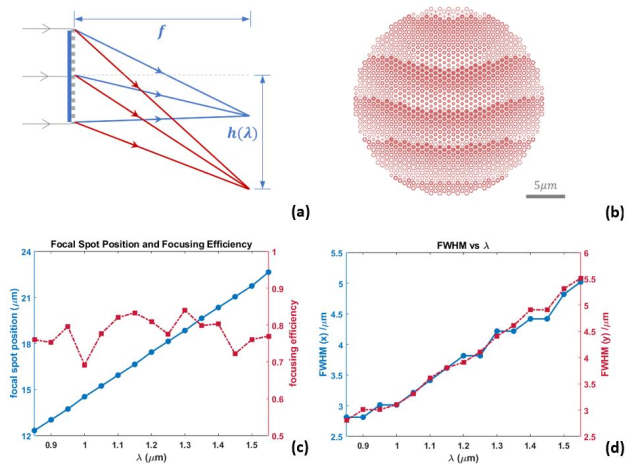
Figure 4. Functional schematic and performance data of the spectral disperser.

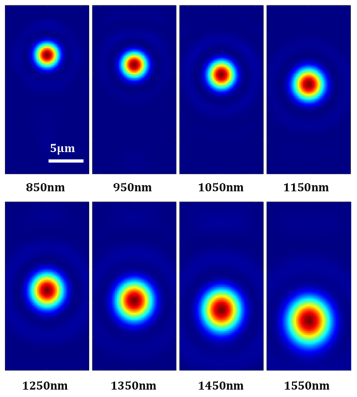
Figure 5. Simulated far-field focusing energy distribution of the spectral disperser.

Key Highlights:

1.The dispersion design method is more refined and effective compared to many complex inverse design methods. The introduction of the nominal parameter concept technically corrects the issue of periodic boundary condition mismatch in the metasurface design process.

2.The design method offers high flexibility, being applicable to both continuous bandwidth and discrete wavelength dispersion design. It is also not limited by the operational wavelength band; for example, it can be used for the visible light spectrum.

3.The design process has considered fabrication feasibility. Furthermore, better design results can be achieved with more advanced fabrication techniques.

Authorship :

Dr. Zhuang Ma, a postdoctoral researcher at Westlake University, is the first author of this study. Professor Wei Yan, a Research Fellow at Westlake University, is the second author. Professor Min Qiu, the principal investigator of the research group, is the corresponding author. 

Source: Westlake University School of Engineering (SOE) Official WeChat Account